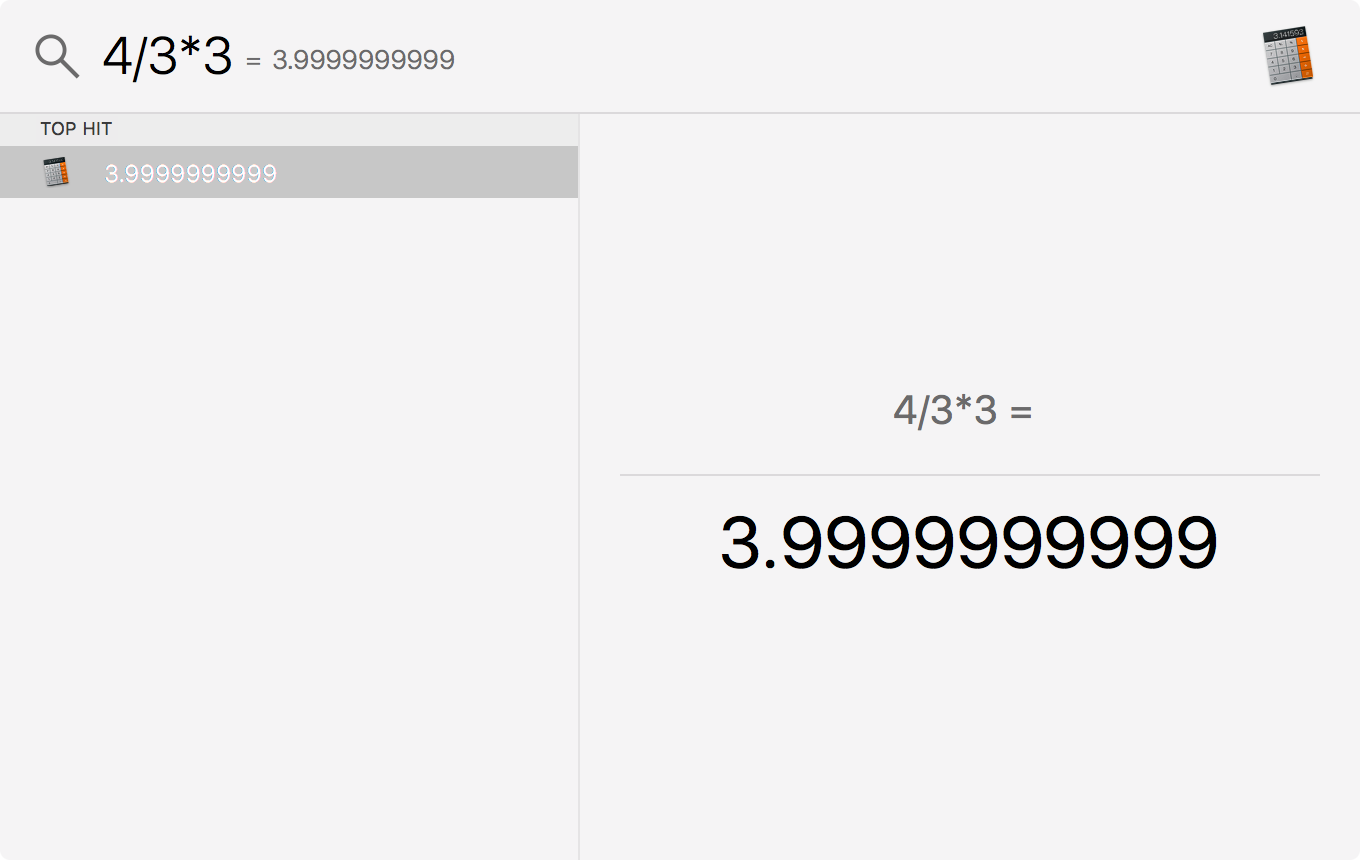
One third of four multiplied by three is not four, according to the OS X calculator. I know this quirk is due to behind the scenes floating point arithmetic, but it’s interesting Apple hasn’t found a way to cosmetically fix this considering this calculator might be the most commonly used one in the world!

4/3*3=3.9999999999

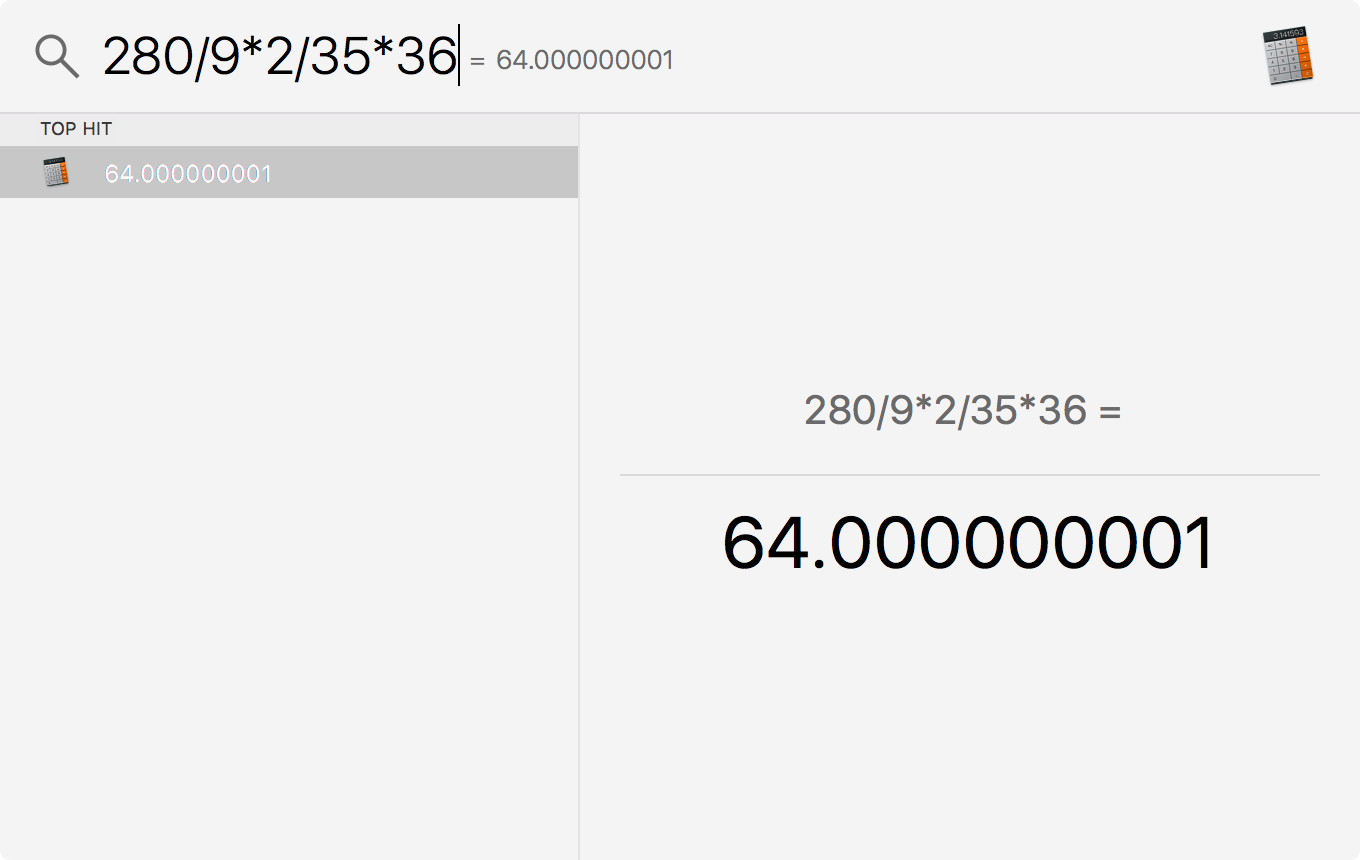
The actual problem I was doing when I noticed this, involving conversion between degrees and radian based area, was 280/9*2/35*36, which computed to 64.000000001.

280/9*2/35*36=64.000000001

I did some permutations on this and found, as suspected, the problem arises when an intermediate calculation results in a large or possibly infinite number of digits following the decimal, and that situation might be avoided simply by rearranging the operations in ways the commutative property allows.

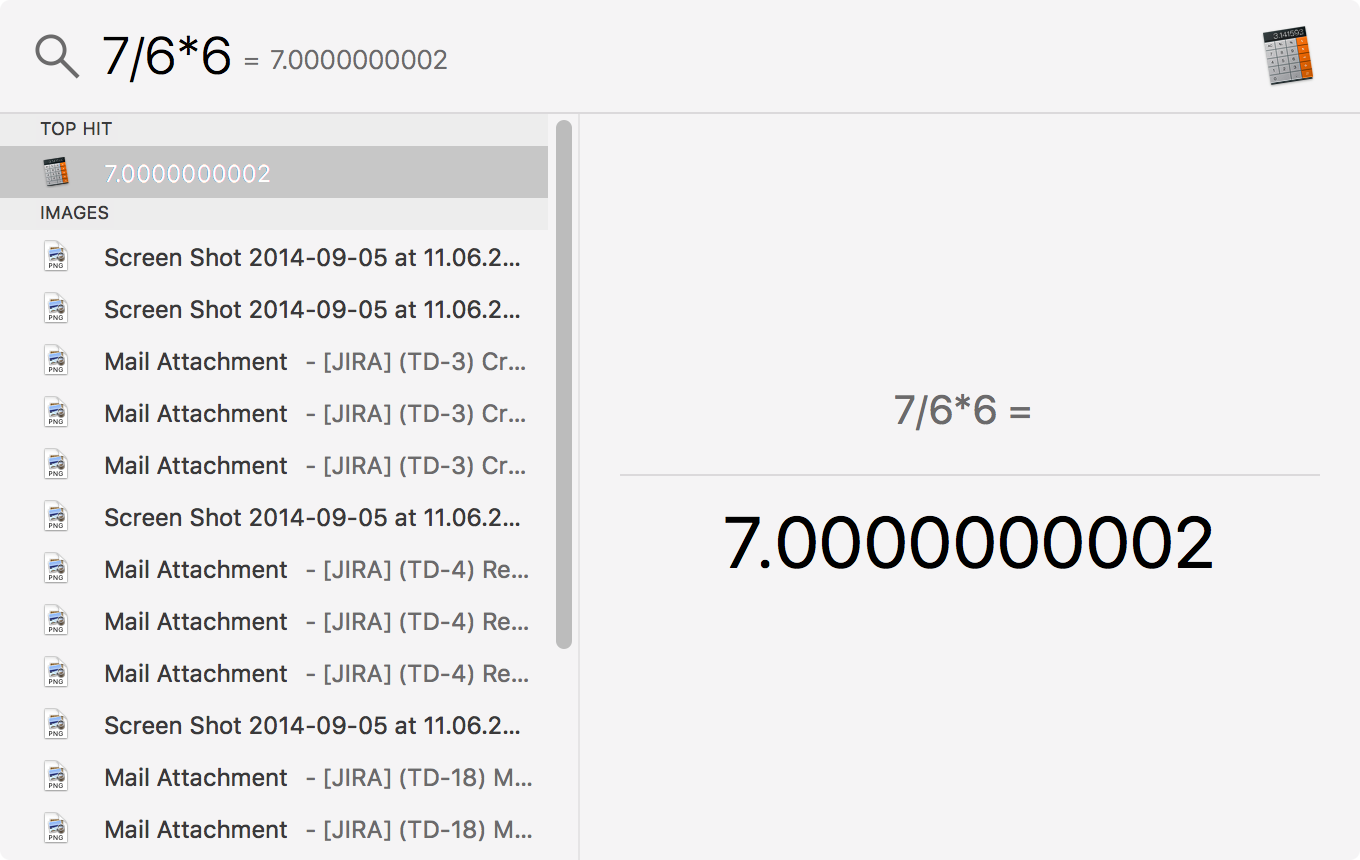
For example, 7*6 is 42, and 42/6 is 7. That has no long decimals. But 7/6 is 1.16666…, and since that apparently cannot be represented exactly by the computer, multiplying again by 6 does not restore the original 7.

7/6*6=7.0000000002

Other examples:

• 8/7*7=8.0000000003
• 10/9*9=9.9999999999
• 16/15*15=16.000000001
• 19/18*18=19.000000001
• 20/19*19=19.999999999
• 23/22*22=23.000000001
• 24/23*23=24.000000001
• 25/24*24=25.000000001
• 27/26*26=27.000000001
• 28/27*27=27.999999999
• 30/29*29=29.999999999
• 560/315*36=64.000000001

At least this problem has a somewhat intuitive cause; we can see that intermediate value has a crazy value that we couldn’t blame a computer for truncating, thus losing precision. Computers also struggle with seemingly simpler problems with decimal subtraction, though Apple and others have addressed these.

A decade ago, Mike Davidson showed some of these in Apple Flunks First Grade Math, where he found 9533.24-.1=9533.139999999999. That problem occurred because the computer simply could not store 0.1 exactly. (In reference to this post’s title, I’m pretty sure multiplication and division aren’t taught in first grade, but I think the same is true of the math Davidson was doing in his post, so I stuck with the theme.)

The Python documentation on Floating Point Arithmetic has a good explanation of this. It boils down to 0.1 is represented in binary by the infinitely repeating fraction 0.00011001100110011..., which is similar to what I observed above, only the intermediate values I was considering were base 10, not base 2 like binary.

The computer ultimately is using binary for those as well, but maybe there are clever ways to resolve the binary repeating decimals employed in the background. It doesn’t seem like that solution simply involves rounding, since that would seem to preclude getting a result with many zeros ending in a one like I observed.

Back to work!